Question

Un punto se ubica en un sistema de coordenadas polar por las coordenadas r = 7.6 m y = 30°. Encuentre las coordenadas x y y de este punto (en m), suponiendo que los dos sistemas de coordenadas tienen el mismo origen.

Answer 1

Las coordenadas del punto son
`(x,y) = (6.582\,m, 3.8\,m)`.

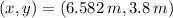Step-by-step explanation:

La relación entre un vector en formato polar y uno con formato rectangular con respecto al mismo origen queda sintetizado por la siguiente expresión:

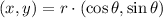`(x, y) = r\cdot (\cos \theta, \sin \theta)` (1)

Donde:

`r` - Magnitud de la distancia del punto con respecto al origen, medido en metros.

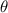`\theta` - Dirección del punto con respecto del semieje +x, medido en grados sexagesimales.

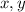`x,y` - Coordenadas rectangulares del punto con respecto al origen, medidas en metros.

Si sabemos que
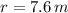`r = 7.6\,m` y
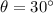`\theta = 30^(\circ)`, entonces las coordenadas rectangulares del punto con respecto al origen son:

`(x,y) = (7.6\,m)\cdot (\cos 30^(\circ), \sin 30^(\circ))`

`(x,y) = (6.582\,m, 3.8\,m)`

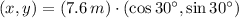
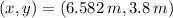
Las coordenadas del punto son
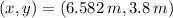`(x,y) = (6.582\,m, 3.8\,m)`.