Question

The area of a rectangle is represented by the polynomial 3x3+14x2-23x+6. The width of the rectangle is represented by the expression x+6. Find the expression that represents the length of the rectangle.

Answer 1

`l=3x^2-4x+1`

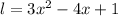
Explanation:

Given that,

The area of a rectangle is,
`A=3x^3+14x^2-23x+6`

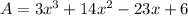
The width of the rectangle, b = (x+6)

We need to find the expression for the length of the rectangle. We know that, the area of a rectangle is given by :

A = lb

Where

l is the length of the rectangle

Put all the values,

`l=(A)/(b)\\\\l=(3x^3+14x^2-23x+6)/((x+6))\\\\l=((x-1)(x+6)(3x-1))/((x+6))\\\\l=(x-1)(3x-1)\\\\=3x^2-4x+1`

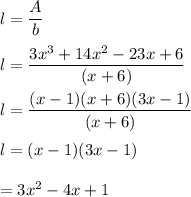
So, the length of the rectangle is equal to
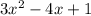`3x^2-4x+1`.