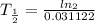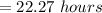Question

An investigator collects a sample of a radioactive isotope with an activity of 490,000 Bq.48 hours later, the activity is 110,000 Bq. Part A For the steps and strategies involved in solving a similar problem, you may view a Video Tutor Solution What is the half-life of the sample?

Answer 1

The correct answer is "22.27 hours".

Step-by-step explanation:

Given that:

Radioactive isotope activity,

= 490,000 Bq

Activity,

= 110,000 Bq

Time,

= 48 hours

As we know,

⇒
`A = A_0 e^(- \lambda t)`

or,

⇒
`(A)/(A_0)=e^(-\lambda t)`

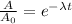
By taking "ln", we get

⇒
`ln (A)/(A_0)=- \lambda t`

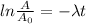
By substituting the values, we get

⇒
`-ln (110000)/(490000) = -48 \lambda`

⇒
`-1.4939=-48 \lambda`

`\lambda = 0.031122`

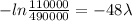
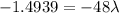
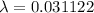
As,

⇒
`\lambda = (ln_2)/((T)/(2) )`

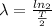
then,

⇒
`(ln_2)/(T_ (1)/(2) ) =0.031122`

⇒
`T_(1)/(2)=(ln_2)/(0.031122)`

`=22.27 \ hours`