The measure of the angle of elevation from Terrance to the top of the tree is 53° is x = 29tan53
What is angle of elevation ?
Particularly in trigonometry, the angle of elevation is an often utilized notion in relation to height and distance. It is described as the angle formed by the observer's eye to an item above his horizontal plane and oblique line. This angle eventually forms above the surface.
Let the Height of the tree = x
Distance from base of the tree = 29feet
Angle of elevation = 53degrees
From trigonometry
tan θ = opposite/adjacent
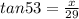
x = 29tan53