Answer:
The current amount of the Potassium-40 sample is approximately 37.521 grams.
Step-by-step explanation:
The amount of the sample of the radioactive isotope decays exponentially in time, the amount of mass of the sample as a function of time (
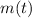 ), in grams, is described below:
), in grams, is described below:
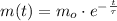 (1)
(1)
Where:
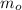 - Initial mass, in grams.
- Initial mass, in grams.
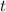 - Time, in years.
- Time, in years.
 - Time constant, in years.
- Time constant, in years.
The time constant can be found from half life (
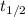 ), in years, described in statement:
), in years, described in statement:
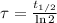 (2)
(2)
If we know that
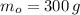 ,
,
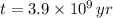 and
and
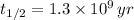 , then the current amount of the sample is:
, then the current amount of the sample is:
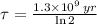
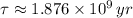
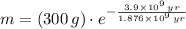
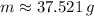
The current amount of the Potassium-40 sample is approximately 37.521 grams.