Given:
Quadrilateral ABCD is similar to Quadrilateral WXYZ.
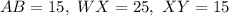 and
and
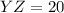 .
.
To find:
The measure of BC.
Solution:
We know that the corresponding sides of similar figures are proportional.
It is given that Quadrilateral ABCD is similar to Quadrilateral WXYZ. It means their corresponding sides are proportional.
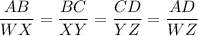
Now,
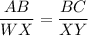
After substituting the given values, we get
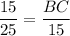
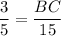
Multiply both sides by 15.
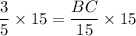
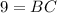
Therefore, the measure of BC is 9 units.