Question

A boy throws a ball straight up with a speed of 21.5 m/s. The ball has a mass of 0.19 kg. How much gravitational potential energy will the ball have at the top of its flight? (Assume there is no air resistance.) A. 43.9 J B. 37.5 J C. 48.5 J D. 41.2 J​

Answer 1

Step-by-step explanation:

The equation fo potential energy is PE = mgh, where m is the mass of the ball, g is the pull of gravity (constant at 9.8), and h is the max height of the ball. What we do not have here is that height. We need to first solve for it using one-dimensional equations. What we have to know above all else, is that the final velocity of an object at its max height is always 0. That allows us to use the equation

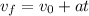`v_f=v_0+at` where vf is the final velocity and v0 is the initial velocity. We will find out how long it takes for the object to reach that max height first and then use that time to find out what that max height is. Baby steps here...

0 = 21.5 + (-9.8)t and

-21.5 = -9.8t so

t = 2.19 seconds (Keep in mind that if I used the rules correctly for sig fig's, the answer you SHOULD get is not one shown, so I had to adjust the sig fig's and break the rules. But you know what they say about rules...)

Now we will use that time to find out the max height of the object in the equation

Δx =
`v_0t+(1)/(2)at^2` and filling in:

Δx =
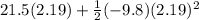`21.5(2.19)+(1)/(2)(-9.8)(2.19)^2` which simplifies down a bit to

Δx = 47.1 - 23.5 so

Δx = 23.6 meters.

Now we can plug that in to the PE equation to find the PE of the object:

PE = (.19)(9.8)(23.6) so

PE = 43.9 J