Question

(-5,-12) find cot???????

Answer 1

In Unit Circle, we know that x-term = cos and y-term = sin

`\large \boxed{(x,y) = (cos \theta , sin \theta)}`

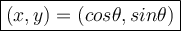
Recall the cotangent ratio:

`\large \boxed{cot \theta = (cos \theta)/(sin \theta) }`

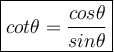
Because cotangent is reciprocal of tangent which is sin/tan so cotangent is 1/(sin/cos) = cos/sin.

Substitute the point in.

`\large{cot \theta = ( - 5)/( - 12 ) \longrightarrow (5)/(12) }`

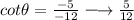
Answer

• cot theta = 5/12

Let me know if you have any doubts!