We've been given to find out the 11th term of a geometric sequence 1,4,16,64...
Here we have,
- Common ratio (r) = 4/1 = 4
The standard formula for calculating the geometric sequence is given by,
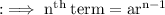
Substituting values we get,
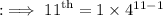
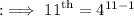
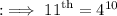
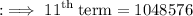
- The 11th term of G.P. is 4¹⁰.