Question

Fine the 11th term of the following geometric sequence 1,4,16,64,​

Answer 1

We've been given to find out the 11th term of a geometric sequence 1,4,16,64...

Here we have,

• First term (a) = 1

• Common ratio (r) = 4/1 = 4

• n = 11

The standard formula for calculating the geometric sequence is given by,

`:\implies\rm{ {n}^(th) \: term = {ar}^(n - 1) }`

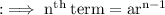
Substituting values we get,

`:\implies\rm{ {11}^(th) = 1 * {4}^(11 - 1) }`

`:\implies\rm{ {11}^(th) = {4}^(11 - 1) }`

`:\implies\rm{ {11}^(th) = {4}^(10) }`

`:\implies\rm{ {11}^(th) \: term = 1048576}`

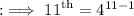
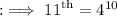
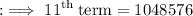
• The 11th term of G.P. is 4¹⁰.

Answer 2

Explanation:

First term = a = 1

common ratio = r = second term ÷ first term = 4 ÷ 1 = 4

nth term =
`ar^(n-1)`

11th terms =
`1*4^(10) = 4^(10)`