Question

Suppose you have $100 of endowment, and you are offered a chance to buy a lottery which costs $36. The lottery has 43% of chance to win a prize of $G, or you just lose and get nothing. Suppose your utility function on wealth is u(w)=w^1/2. What is the least prize size G that you will be willing to buy the lottery? (Round to the second digit after decimal point.)

Answer 1

96.02

Step-by-step explanation:

Lottery's Expected utility =
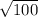`√(100)` = 10

Income in good state = 100 - 36 + G = 64 + G

Income in bad state = 100 - 36 = 64

Probability in good state = 43%

Probability in bad state = 100% - 43% = 57%

Expected utility = Probability in good state x
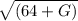`√((64 + G ))` + Probability in bad state x
`√(64\\)`

10 = 43% x
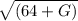`√((64 + G ))` + 57% x 8

10 = 43% x
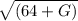`√((64 + G ))` + 4.56

10 - 4.56 = 43% x
`√((64 + G ))`

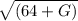
5.44 = = 43% x
`√((64 + G ))`

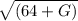
5.44 / 43% =
`√((64 + G ))`

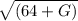
12.65 =
`√((64 + G ))`

`12.65^(2)` =
`(√((64 + G )))^(2)`

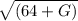
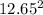160.0225 = 64 + G

G = 160.0225 - 64

G = 96.0225

G = 96.02