Question

HELP TIMER Write the equation of a hyperbola centered at the origin with x-intercept +/- 4 and foci of +/-2(squareroot 5)

Answer 1

Given:

x-intercepts of the hyperbola are ±4.

The foci of hyperbola are
`\pm 2√(5)`.

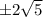Center of the hyperbola is at origin.

To find:

The equation of the hyperbola.

Solution:

The general equation of a hyperbola:

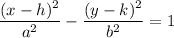`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1` ...(i)

Where, (h,k) is the center of the hyperbola, ±a are x-intercepts,
`(\pm c,0)` are foci.

Center of the hyperbola is at origin. So, h=0 and k=0.

x-intercepts of the hyperbola are ±4. So,

`\pm a=\pm 4`

`a=4`

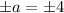
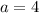
The foci of hyperbola are
`\pm 2√(5)`.

`\pm c=\pm 2√(5)`

`c=2√(5)`

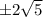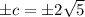
We know that,

`a^2+b^2=c^2`

`(4)^2+b^2=(2√(5))^2`

`16+b^2=20`

`b^2=20-16`

`b^2=4`

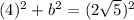
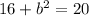
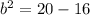
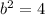
Taking square root on both sides, we get

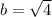`b=√(4)` [b>0]

`b=2`

Substituting
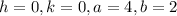`h=0,k=0,a=4,b=2` in (i), we get

`((x-0)^2)/(4^2)-((y-0)^2)/(2^2)=1`

`(x^2)/(4^2)-(y^2)/(2^2)=1`

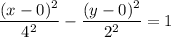
Therefore, the correct option is (d).