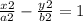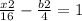Question

HELP TIMER Write the equation of a hyperbola centered at the origin with x-intercept +/- 4 and foci of +/-2(squareroot 5)

Answer 1

`(x2)/(a) - (y2)/(b2) = 1`

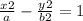
Explanation:

A hyperbola is the locus of a point such that its distance from a point to two points (known as foci) is a positive constant.

The standard equation of a hyperbola centered at the origin with transverse on the x axis is given as:

`(X2)/(16) - (b)/(4) = 1`

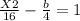
The coordinates of the foci is at (±c, 0), where c² = a² + b²

Given that a hyperbola centered at the origin with x-intercepts +/- 4 and foci of +/-2√5. Since the x intercept is ±4, this means that at y = 0, x = 4. Substituting in the standard equation:

I don't feel like explaining so...

a. = 4

The foci c is at +/-2√5, using c² = a² + b²:

B = 2

Substituting the value of a and b to get the equation of the hyperbola:

`(x2)/(a2) - (y2)/(b2) = 1`

`(x2)/(16) - (b2)/(4) = 1`