Answer:
A two column proof is presented as follows;
Statement
 Reason
Reason
1. AB ║ DE, BD bisects AE
 Given
Given
2. ∠BAE = ∠AED, ∠ABD = ∠BDA
 Alternate ∠s are equal
Alternate ∠s are equal
3.
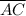 =
=
 ,
,
 =
=
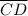

 By definition of bisection of line AE by BD
By definition of bisection of line AE by BD
4. ΔABC ≅ ΔEDC
 By SAA, rule of congruency
By SAA, rule of congruency
Explanation:
Step 1. AB ║ DE, BD bisects AE
 Given
Given
Step 2. ∠BAE , ∠AED, and ∠ABD, ∠BDA
 are pairs of alternate angles formed by the parallel lines, AB and DE and are therefore, equal
are pairs of alternate angles formed by the parallel lines, AB and DE and are therefore, equal
Step 3.
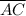 =
=
 ,
,
 =
=
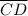 The bisection of line gives two lines of equal length. The bisection of AE by BD gives,
The bisection of line gives two lines of equal length. The bisection of AE by BD gives,
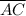 and
and
 where
where
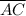 =
=

Similarly, the bisection of BD by AE gives,
 and
and
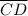 , where
, where
 =
=
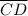
Step 4. ΔABC ≅ ΔEDC
 By the Side-Angle-Angle (SAA), rule of congruency, which states that two triangles having two angles and the corresponding non included sides of each triangle equal to the other, the two triangles are congruent.
By the Side-Angle-Angle (SAA), rule of congruency, which states that two triangles having two angles and the corresponding non included sides of each triangle equal to the other, the two triangles are congruent.