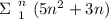Question

Write the following series in sigma notation. 8+18+28+38

Answer 1

`\Sigma\left {n} \atop {1}} \right. (5n^2+3n)`

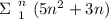
Explanation:

Given the series 8 + 18 + 28 + 38

First, we need to find the sum of the nth term of the sequence as shown

Sn = n/2[2a+(n-1)d]

n is the number of terms

a is the first term = 8

d is the common difference = 18-8 = 28-18 = 10

Substitute

Sn = n/2 [2(8)+(n-1)*10]

Sn = n/2 [16+10n-10]

Sn = n/2[10n+6]

Sn = 2n/2(5n+3)

Sn = n(5n+3)

Sn = 5n²+3n

In Sigma form;

`\Sigma\left {n} \atop {1}} \right. (5n^2+3n)`