Question

Right triangle XYZ has right angle Z. If the sin(X)=1213
, what is the cos(X)

Answer 1

Given:

Right triangle XYZ has right angle Z.

`\sin(x)=(12)/(13)`

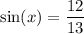
To find:

The value of
`\cos x`.

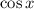Solution:

We know that,

`\sin^2(x)+\cos^2(x)=1`

`\cos^2(x)=1-\sin^2(x)`

`\cos(x)=\pm√(1-\sin^2x)`

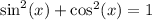
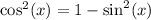
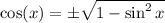
For a triangle, all trigonometric ratios are positive. So,

`\cos(x)=√(1-\sin^2x)`

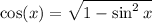
It is given that
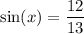`\sin(x)=(12)/(13)`. After substituting this value in the above equation, we get

`\cos(x)=\sqrt{1-((12)/(13))^2}`

`\cos(x)=\sqrt{1-(144)/(169)}`

`\cos(x)=\sqrt{(169-144)/(169)}`

`\cos(x)=\sqrt{(25)/(169)}`

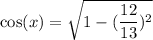
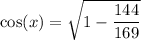
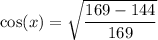
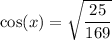
On further simplification, we get

`\cos(x)=(√(25))/(√(169))`

`\cos(x)=(5)/(13)`

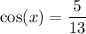
Therefore, the required value is
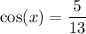`\cos(x)=(5)/(13)`.