Question

What is the height of the pyramid ???

Answers:
A: 7cm
B: 5cm
C: 14 cm
D: 10 cm

Answer 1

Given:

`m\angle ACD=45^\circ`

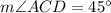
Point B is the center of the base.

Each side of the base = 10 cm

To find:

The height of the pyramid.

Solution:

It is given that the measure of each side of the base is 10 cm. It means the base is square. The length of the diagonal of a square is:

`d=a√(2)`

Where, a is the side length of the square.

Putting
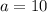`a=10` in the above formula, we get

`d=10√(2)`

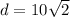
It is given that point B is the center of the base. It means point B bisect each diagonal of a base. So,

`BC=(d)/(2)`

`BC=(10√(2))/(2)`

`BC=5√(2)`

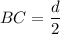
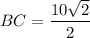
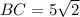
In a right angle triangle,

`\tan \theta=(Perpendicular)/(Base)`

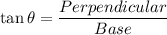
In triangle ABC,

`\tan (45^\circ)=(AB)/(BC)`

`1=(h)/(5√(2))`

`5√(2)=h`

`7.0710678=h`

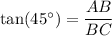
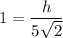
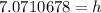
Round the value to the nearest integer.

`h\approx 7`

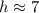
The height of the pyramid is about 7 cm. Therefore, the correct option is A.