Answer:
X1 =
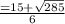 and X2 =
and X2 =
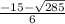
Explanation:
To find the roots of a quadratic equation, you need to solve the quadratic equation by using the quadratic formula.
OR
You can use the (Equation/Function) mode on the calculator.

For this equation,
a = 3
b = 15
c = -5
X1 =
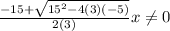
X2 =
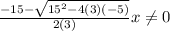
Solving this on the calculator and you should get
X1 =
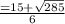 X2 =
X2 =
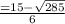
a, b, c = constants, where a ≠ 0
x = the unknown