Question

Find the length of the third side if necessary right in simplest radical form

Answer 1

`\large{ \tt{❃ \: SOLUTION}} :`

• The longest side , which is the opposite of side of right angle is the hypotenuse ( h ). There are two other sides, the perpendicular ( p ) and the base ( b ) .

• In given right triangle , hypotenuse ( h ) =
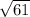  `√(61)` , perpendicular ( p ) = 5 & base ( b ) = ?

`\large{ \tt{✻ \: USING \: PYTHAGOREAN\: THEOREM : }}`

`\large{ \tt{❁ {h}^(2) = {p}^(2) + {b}^(2) }}`

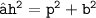
• Plug the values and simplify!

`\large{ ↦( √(61) })^(2) = {5}^(2) + {b}^(2)`

`\large{↦ \: 61 = 25 + {b}^(2) }`

`\large{↦25 + {b}^(2) = 61 }`

`\large{↦ {b}^(2) = 61 - 25}`

`\large{↦ {b}^(2) = 36}`

`\large{↦ {b} = √(36) }`

`\large{↦ b = \sqrt{ \underline{3 * 3} * \underline{ 2 * 2} }}`

`\large{↦b = 3 * 2}`

`\large{ \boxed{ \boxed{ \bold{↦b = 6 \: units }}}}`

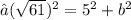
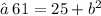
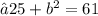
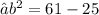
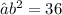
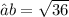
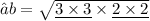
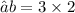
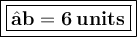
• Hence , the length of a third side is
  `\boxed{ \tt{6 }}` units .

✺ Never give up on something that you actually want !

۵Hope I helped! ツ

☼ Have a wonderful day / night ! ☃

# StayInAndExplore ! ☂

▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁

Answer 2

___________________________________

Problem:

• Find the length of the third side if necessary right in simplest radical form.

Formula:

`\quad\quad\quad\quad\boxed{\tt{ {c}^(2) = \sqrt{ {a}^(2) + {b}^(2) }}}`

Remember:

• a = perpendicular
• b = base
• c = hypotenuse

Given:

`\quad\quad\quad\quad\tt{ a = 5 }`

`\quad\quad\quad\quad\tt{ b = ? }`

`\quad\quad\quad\quad\tt{ {c = √(61) }}`

Solution:

`\quad\quad\quad\quad\tt{ {( √(61)) }^(2) = \sqrt{ {(5)}^(2) + {b}^(2) }}`

`\quad\quad\quad\quad\tt{ {61}= \sqrt{ {25} + {b}^(2) }}`

`\quad\quad\quad\quad\tt{ 61 = \sqrt{ 25 + {b}}}`

• Let's convert the "b" like this.

`\quad\quad\quad\quad\tt{ {b } = √(25 - 61 )}`

`\quad\quad\quad\quad\tt{ {b } = √(36 )}`

`\quad\quad\quad\quad\tt{ {b } = 6 }`

So the final answer is:

`\quad\quad\quad\quad \boxed {\boxed{\tt{ \color{magenta} {b } = 6\:units }}}`

___________________________________

#CarryOnLearning

✍︎ C.Rose❀