Answer:
It does not form a linear equation.
Explanation:
For this question, you should check that they all have the same gradient.
To work out the gradient, use
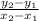 .
.
Using the top 2 rows, this gives
 , or
, or
 , simplified to
, simplified to
 . This means for every increase in x by 1, y increases by
. This means for every increase in x by 1, y increases by
 .
.
Between the first 2 rows, x increases by 4 and y by 2 (half of 4), so it is true.
Between the second and third rows, x increases by 2 and y by 2 (which isn't half of 2). This is false, meaning this does not form a linear equation.
**This question involves solving linear equations using gradients, which you may want to revise. I'm always happy to help!