Question

You are in charge of monitoring the pressure of a compressed air tank in a processing plant. After repeating the pressure measurement a large number of times, you found that the pressure values have Gaussian distribution with a mean value of 69 psi and a standard deviation of 10 psi. If it is important that the pressure stays below 84 psi, what is the probability (in percent) that the pressure will exceed this value

Answer 1

11.5

Explanation:

Given that :

I am in charge of the pressure reading in a compressed air tank of a processing plant.

The Gaussian distribution having a mean value = 69 psi

Standard deviation = 10 psi

Here we have to find the probability that the pressure will exceed 84 psi.

So,

`P(X \geq 84) = P \left((X - 69)/(10) > (84-69)/(10) \right)`

`$=P(Z > 1.5)$`

`$=1-P(Z < 1.5)$`

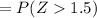
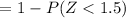
= 0.115

= 11.5