Answer:
Distance:
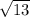 units
units
Explanation:
The distance formula is
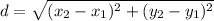 where:
where:
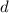 is the distance between points
is the distance between points
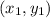 and
and
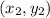
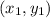 are the coordinates of the first point
are the coordinates of the first point
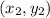 are the coordinates of the second point
are the coordinates of the second point
We are given that:
To determine the value of our distance,
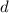 , we plug in our given information into the formula and solve for
, we plug in our given information into the formula and solve for
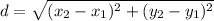
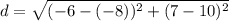
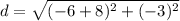
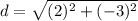
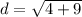
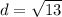
Therefore, the distance between
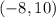 and
and
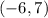 is
is
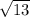 units.
units.
See the attached graph for a visual.