Question

For the function f(x) = x23, the average rate of change to the nearest hundredth over the interval 2 d x d 4 is

Answer 1

Given:

Consider the function is:

`f(x)=(x^2)/(3)`

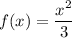
To find:

The average rate of change over the interval 2 ≤ x ≤ 4.

Solution:

We have,

`f(x)=(x^2)/(3)`

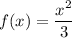
At
`x=2`,

`f(2)=(2^2)/(3)`

`f(2)=(4)/(3)`

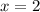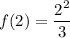
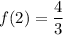
At
`x=4`,

`f(4)=(4^2)/(3)`

`f(4)=(16)/(3)`

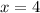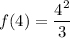
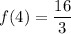
The average rate of change of a function f(x) over the interval [a,b] is:

`m=(f(b)-f(a))/(b-a)`

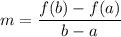
So, the average rate of change over the interval 2 ≤ x ≤ 4 is:

`m=(f(4)-f(2))/(4-2)`

`m=((16)/(3)-(4)/(3))/(2)`

`m=((16-4)/(3))/(2)`

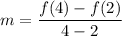
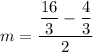
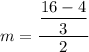
On further simplification, we get

`m=(12)/(3* 2)`

`m=(12)/(6)`

`m=2`

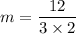
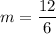
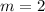
Therefore, the average rate of change over the interval 2 ≤ x ≤ 4 is 2.