Question

the average amount of time a person exercises daily is 22.7 minutes in a population. A random sample of 20 people showed an average of 29.8 minutes in time with a standard deviation of 9.8 minutes. At alpha=0.01, can it be concluded that the average differs from the population average?

Answer 1

The p-value of the test is 0.0043 < 0.01, which means that it can be concluded that the average differs from the population average.

Explanation:

The average amount of time a person exercises daily is 22.7 minutes in a population. Test if the average differs from the population average.

At the null hypothesis, we test if it does not differ, that is, the mean is of 22.7 minutes. So

`H_0: \mu = 22.7`

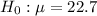
At the alternate hypothesis, we test if it does differ, that is, if the mean is different of 22.7 minutes. So

`H_1: \mu \\eq 22.7`

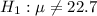
The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.

22.7 is tested at the null hypothesis:

This means that
`\mu = 22.7`

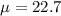
A random sample of 20 people showed an average of 29.8 minutes in time with a standard deviation of 9.8 minutes.

This means that
`n = 20, X = 29.8, s = 9.8`

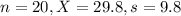
Value of the test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (29.8 - 22.7)/((9.8)/(√(20)))`

`t = 3.24`

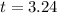
P-value of the test:

Using the t-distribution, testing if the mean is different, so a two-tailed test with t = 3.24 and 20 - 1 = 19 degrees of freedom.

Using a t-distribution calculator, the p-value of the test is of 0.0043.

The p-value of the test is 0.0043 < 0.01, which means that it can be concluded that the average differs from the population average.