Question

We are drawing a 5-card hand from a standard 52-card deck a. What is the probability that all the cards are spades? (5pts)

Answer 1

0.0005 = 0.05% probability that all the cards are spades.

Explanation:

The cards are chosen without replacement, which means that the hypergeometric distribution is used to solve this question.

Hypergeometric distribution:

The probability of x sucesses is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

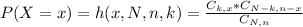
In which:

x is the number of sucesses.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

In this question:

52 cards means that N = 52.

13 of the cards are spades, which means that k = 13.

5 card hand means that n = 5.

What is the probability that all the cards are spades?

This is P(X = 5). So

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

`P(X = 5) = h(5,52,5,13) = (C_(13,5)*C_(39,0))/(C_(52,5)) = 0.0005`

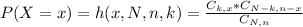
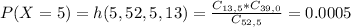
0.0005 = 0.05% probability that all the cards are spades.