Question

Which set is closed under subtractionWhich answer choice shows that the set of irrational numbers is not closed under addition

Answer 1

(a) Set of rational numbers

(b)
`\pi + (-\pi) = 0`

Explanation:

Solving (a): Set that is closed under subtraction

The solution to this is rational numbers.

For a set of number to be closed under subtraction, the following condition must be true

`a -b = c`

Where

a, b, c are of the same set.

The above is only true for rational numbers.

e.g.

`1 - 2 = -1`

`5 - 5 = 0`

`(1)/(2) - (1)/(4) = (1)/(2)`

`4 - 2 = 2`

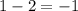
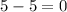
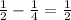
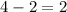
The operations and the result in the above samples are rational numbers.

Solving (b): Choice not close under addition[See attachment for options]

As stated in (a)

For a set of number to be closed under subtraction, the following condition must be true

`a -b = c`

Where

a, b, c are of the same set.

In the given options (a) to (d), only

`\pi + (-\pi) = 0` is not close under addition because:

`\pi` is irrational while
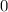`0` is rational

In other words, they belong to different set