Question

a. Fill in the midpoint of each class in the column provided. b. Enter the midpoints in L1 and the frequencies in L2, and use 1-VarStats to calculate the mean and standard deviation of the frequency distribution (see section 3.2 if needed). Using the frequency distribution, I found the mean height to be _______________ with a standard deviation of _______________.

Answer 1

`\begin{array}{ccc}{Midpoint} & {Class} & {Frequency} & {64} & {63-65} & {1} & {67} & {66-68} & {11} & {70} & {69-71} & {8} &{73} & {72-74} & {7} & {76} & {75-77} & {3} & {79} & {78-80} & {1}\ \end{array}`

Using the frequency distribution, I found the mean height to be 70.2903 with a standard deviation of 3.5795

Explanation:

Given

See attachment for class

Solving (a): Fill the midpoint of each class.

Midpoint (M) is calculated as:

`M = (1)/(2)(Lower + Upper)`

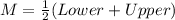
Where

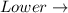`Lower \to` Lower class interval

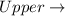`Upper \to` Upper class interval

So, we have:

Class 63-65:

`M = (1)/(2)(63 + 65) = 64`

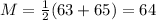
Class 66 - 68:

`M = (1)/(2)(66 + 68) = 67`

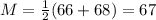
When the computation is completed, the frequency distribution will be:

`\begin{array}{ccc}{Midpoint} & {Class} & {Frequency} & {64} & {63-65} & {1} & {67} & {66-68} & {11} & {70} & {69-71} & {8} &{73} & {72-74} & {7} & {76} & {75-77} & {3} & {79} & {78-80} & {1}\ \end{array}`

Solving (b): Mean and standard deviation using 1-VarStats

Using 1-VarStats, the solution is:

`\bar x = 70.2903`

`\sigma = 3.5795`

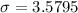
See attachment for result of 1-VarStats