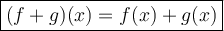
The property above is distribution property where we distribute x-term in the function.
Substitute both f(x) and g(x) in.
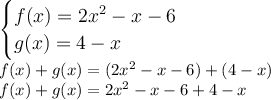
Évaluate/Combine like terms.
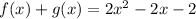
The function can be factored so there are two answers. (Both of them work as one of them is factored form while the other one is not.)
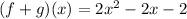
Alternative
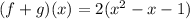
Answer
- (f+g)(x) = 2x²-2x-2
- (f+g)(x) = 2(x²-x-1)
Both answers work. The second answer is in factored form.
Let me know if you have any doubts!