Given the system of equations below:
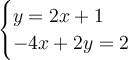
The first equation is y-isolated so we can substitute in the second equation.

Use the distribution property to expand in and simplify.
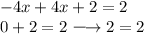
The another method is to divide the second equation by 2.
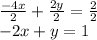
Arrange in the form of y = mx+b.

When we finally arrange, compare the equation to the first equation. Both equations are the same which mean that both graphs are also same and intersect each others infinitely.
For more information, when the both sides are equal for equation - the answer would be infinitely many. If both sides aren't equal (0 = 4 for example) - the answer would be none. If the equation can be solved for a variable then it'd be one solution.
Answer
Hope this helps. Let me know if you have any doubts!