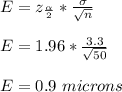Question

Felix is a quality control expert at a factory that paints car parts. Their painting process consists of a primer coat, color coat, and clear coat. For a certain part, these layers have a combined target thickness of 150 microns. Felix measured the thickness of 50 randomly selected points on one of these parts to see if it was painted properly. What is Felix's margin of error? "Round to 2 decimal places​

Answer 1

0.9

Explanation:

His sample had a mean thickness of 148 microns and a standard deviation of 3.3 microns with a 95% confidence interval for the mean thickness.

Solution:

The z score shows by how many standard deviations the raw score is above or below the mean.

Given that:

The mean (μ) = 148 microns, standard deviation (σ) = 3.3 microns, sample size (n) = 50 and confidence interval (C) = 95%

α = 1 - C = 1 - 0.95 = 0.05

α/2 = 0.05/2 = 0.025

The z score of α/2 is the same as the z score of 0.475 (1 - 0.025) which is equal to 1.96

The margin of error (E) is given by:

`E=z_{(\alpha)/(2) }*(\sigma)/(√(n) ) \\\\E=1.96*(3.3)/(√(50) ) \\\\E=0.9\ microns`