Given:
z varies directly with x and inversely with y, when x = 2, y = 5, and z = 10.
To find:
The value of z when x=3 and y=15.
Solution:
It is given that z varies directly with x and inversely with y. So,
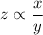
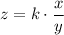 ...(i)
...(i)
Where k is the constant of proportionality.
We have x = 2, y = 5, and z = 10. After substituting these values, we get
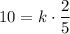
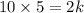
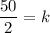
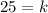
The value of k is 25. After substituting k=25 in (i), we get
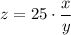 ...(ii)
...(ii)
We need to find the value of z when x=3 and y=15. Substituting x=3 and y=15 in (ii), we get
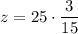
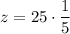
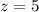
Therefore, the value of z is 5 when x = 3 and y = 15.