Given:
Initial value = 400
Interest rate = 5% compounded quarterly.
To find:
The function that gives you the amount of money in dollars, J(t) in t years after the initial deposit.
Solution:
The formula for amount is:
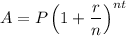
Where, P is principal, r is the rate of interest in decimals, n is the number of times interest compounded in an year and t is the number of years.
The interest rate is 5% compounded quarterly. So, r=0.05 and n=4.
Substituting
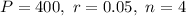 in the above formula, we get
in the above formula, we get
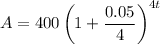
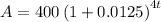
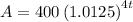
The required function notation is:

Therefore, the amount of money in dollars, J(t) in t years after the initial deposit is
 .
.