The question is incomplete. The complete question is :
Suppose that the Phillips curve is given by :
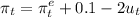
a). What is the natural rate of unemployment ?
Assuming
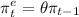 , and suppose that
, and suppose that
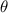 is initially equal to 0. Suppose that the rate of unemployment is initially equal to the natural rate. In year t, the authorities decide to bring the unemployment rate down to 3% and hold it there forever.
is initially equal to 0. Suppose that the rate of unemployment is initially equal to the natural rate. In year t, the authorities decide to bring the unemployment rate down to 3% and hold it there forever.
b). Determine the rate of inflation in years t, t+1, t+2 and t+5.
c). Do you believe the answer given in (b)? Why or why not?
Solution :
Given the equation :
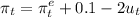
a). At
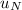 ,
,
 (Inflationary exponents are constant)
(Inflationary exponents are constant)
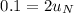
∴
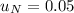
= 5%
b).

Let
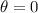 , then
, then
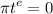 ,
,
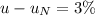
Now for year t
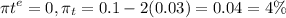
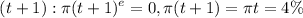

c). No, I do not believe as
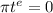 , but πt comes out to be 4%,
, but πt comes out to be 4%,
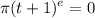 but
but
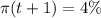 .
.
If inflation is consistently positive, why to make the expectations of zero percentage.