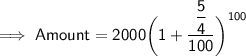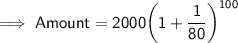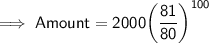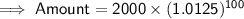We know that, Amount in Compound interest is given by :
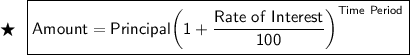
Given : Principal = $2000
Given : Annual yield is 5% and the interest is compounded quarterly
It means : Interest is compounded 4 times in a year

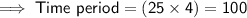
Substituting all the values in the formula, we get :