Question

Let XX be a random variable that is equal to the number of heads in two flips of a fair coin. What is \text E[X^2]E[X 2 ]

Answer 1

Explanation:

From the given information, it is likely that the random variable(X) have the values below:

Let head be H

Let tail be T

So;

X(HH) = 2;

X(HT) = 1;

X(TH) = 1;

X(TT) = 0

The distribution can now be computed as:

`p(X= TT) = (1)/(4)`

`p(X=TH) = (1)/(4)`

`p(X=HT) = (1)/(4)`

`p(X=HH)= (1)/(4)`

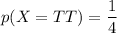
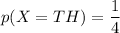
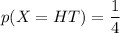
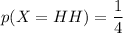
Now, the expected value that is equivalent to the number of heads when the coin is flipped twice is:

`E(X) = p(TT)*X(TT)+p(TH)*X(TH)+p(HT)*X(HT)+p(HH)*X(HH)`

`E(X) = (1)/(4)* 0 + (1)/(4)* 1 + (1)/(4)* 1 + (1)/(4)* 2`

`E(X) = 0 + (1)/(4)+ (1)/(4) + (1)/(2)`

`E(X) =(1+1+2)/(4)`

`E(X) =(4)/(4)`

E(X) = 1

`E(X^2) = p(TT)*X(TT)^2+p(TH)*X(TH)^2+p(HT)*X(HT)^2+p(HH)*X(HH)^2`

`E(X^2) = (1)/(4)* 0^2+ (1)/(4)* 1^2 + (1)/(4)* 1^2 + (1)/(4)* 2^2`

`E(X^2) = 0 + (1)/(4)+ (1)/(4) + (4)/(4)`

`E(X^2) =(1+1+4)/(4)`

`E(X^2) =(6)/(4)`

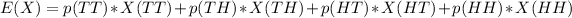
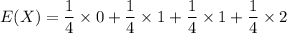
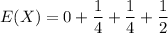
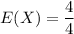
`E(X^2) =1.5`

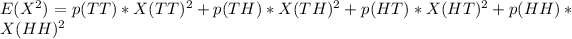
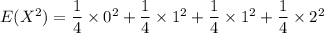
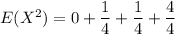
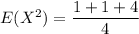
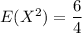
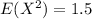
Finally; To compute E²[X]

E²[X] = E[X]²

E²[X] = 1²

E²[X] = 1