Question

In a portfolio problem, X1, X2, and X3 represent the number of shares purchased of stocks 1, 2, and 3, which have selling prices of $15, $47.25, and $110, respectively. The investor has up to $50,000 to invest. The stockbroker suggests limiting the investments so that no more than $10,000 is invested in stock 2 or the total number of shares of stocks 2 and 3 does not exceed 350, whichever is more restrictive. How would this be formulated as a linear programming constraint

Answer 1

The correct solution is "
`x_1 \leq 0.35 (x_1 + x_2 + x_3)`".

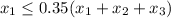Step-by-step explanation:

According to the question,

Let,

For stock 1,

The number of shares to be purchased will be "
`x_1`".

For stock 2,

The number of shares to be purchased will be "
`x_2`".

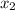For stock 3,

The number of shares to be purchased will be "
`x_3`".

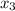then,

The cumulative number of shares throughout stock 1 would be well over or equivalent towards the approximate amount of all the shares or stocks for the set limit.

i.e.,
`x_1+x_2+x_3`

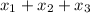
Thus the correct equation is "
`x_1 \leq 0.35(x_1+x_2+x_3)`".