Question

The figure below shows a round plate that is white with a 2-inch gray border around it

What is the area of just the gray border?

Answer 1

Given:

Radius of small circle = 4 in.

Width of gray border = 2 in.

To find:

The area of the gray border.

Solution:

We have, radius of small circle:

`r=4\text{ in.}`

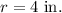
The width of gray border is 2 in. So,t he radius of the larger circle is:

`R=4+2\text{ in.}`

`R=6\text{ in.}`

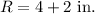
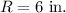
Now, area of gray border is the difference for area of larger circle and smaller circle.

`A=\pi R^2-\pi r^2`

`A=\pi (R^2-r^2)`

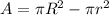
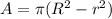
Substituting
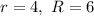`r=4,\ R=6` in the above formula, we get

`A=\pi (6^2-4^2)`

`A=\pi (36-16)`

`A=\pi (20)`

`A=20\pi`

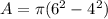
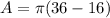
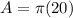
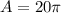
The area of the gray border is
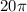`20\pi` square inches. Therefore, the correct option is D.