Question

What would be the best first step in solving this system?

x^2-x+3y=5
x=2y-1

A. Isolate y in the second equation

B. Substitute for x in the first equation

C. Isolate x in the first equation

D. Substitute for y in the second equation

Answer 1

B. Substitute for x in the first equation

Explanation:

The solution to a system of equations in which one is quadratic and the other is linear will necessarily involve solving a quadratic equation. Generally, we want to arrive at that quadratic as early as possible in the solution process.

Here, we have a linear expression for x, so it is pretty simple to use that to substitute for x in the first equation:

(2y -1)² -(2y -1) +3y = 5 . . . . substitute for x

4y² -4y +1 -2y +1 +3y = 5 . . . . eliminate parentheses

4y² -3y -3 = 0 . . . . quadratic in y in standard form

This does not have integer solutions, so it is perhaps best solved using the quadratic formula.

`y=(-(-3)\pm√((-3)^2-4(4)(-3)))/(2(4))=(3\pm√(57))/(8)`

__

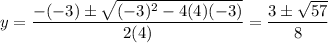
Additional comment

A best first step might be to input both equations to a graphing calculator and let it show you the solutions.