Question

Find all solutions of the equation in the interval [0, 2pi).

- 4 sinx= -cos²x+1
Write your answer in radians in terms of pi.
If there is more than one solution, separate them with commas.

Answer 1

x = 0 , π

Explanation:

`-4 \sin x = 1 - cos^2 x`

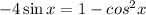
• Rewrite it by using the identity
  `\sin^2x + \cos^2x = 1`

`=> -4\sin x = \sin^2x`

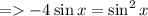
• Add 4sin x to both the sides.

`=> -4\sin x + 4\sin x = sin^2x + 4\sin x`

`=> \sin^2x + 4\sin x = 0`

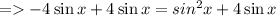
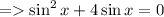
• Take sin x common from the expression in L.H.S.

`=> \sin x(\sin x + 4)=0`

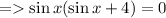
Here , we can get two more equations to find x.

1)
`\sin x(\sin x + 4)=0`

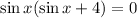
• Divide both the sides by sin x

`=> (\sin x(\sin x + 4))/(\sin x) = (0)/(\sin x)`

`=> \sin x + 4 = 0`

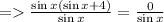
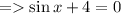
• Substract 4 from both the sides.

`=> \sin x + 4 - 4 = 0 - 4`

`=> \sin x = -4`

`=> x = No \; Solution`

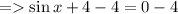
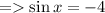
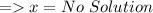
2)
`\sin x(\sin x + 4)=0`

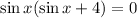
• Divide both the sides by (sin x + 4)

`=> (\sin x(\sin x + 4))/(\sin x + 4) = (0)/(\sin x + 4)`

`=> \sin x = 0`

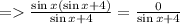
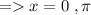`=> x = 0 \; , \pi` over interval [0 , 2π).