Question

Helpppppppppppppp:))))

Answer 1

Given:

Principal value = $1500

Rate of interest = 7% per annum compounded daily

Time = 2 years.

To find:

The amount after 2 years.

Solution:

Formula for amount:

`A=P\left(1+(r)/(n)\right)^(nt)`

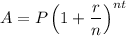
Where, P is principal, r is the rate of interest in decimals, n is the number of time interest compounded in an year and t is the number of years.

We know that 1 year is equal to 365 days and the interest compounded daily. So, n=365.

Substituting
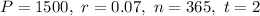`P=1500,\ r=0.07,\ n=365,\ t=2` in the above formula, we get

`A=1500\left(1+(0.07)/(365)\right)^(365(2))`

`A=1500\left((365+0.07)/(365)\right)^(730)`

`A=1500\left((365.07)/(365)\right)^(730)`

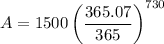
Using calculator, we get

`A\approx 1725.39`

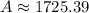
The amount after two years is $1,725.39. Therefore, the correct option is (c).