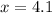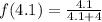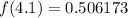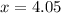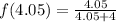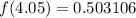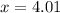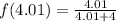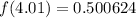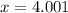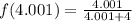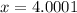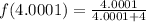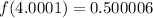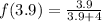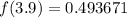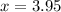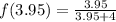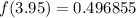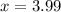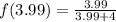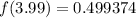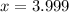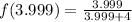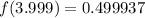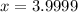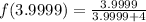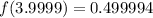Answer:
The function
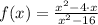 has the following set of solutions:
has the following set of solutions:
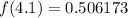 ,
,
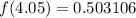 ,
,
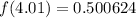 ,
,
 ,
,
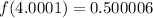 ,
,
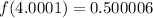
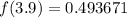 ,
,
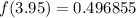 ,
,
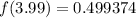 ,
,
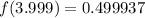 ,
,
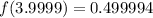
Explanation:
Let be
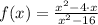 , we proceed to simplify the expression by Algebraic means:
, we proceed to simplify the expression by Algebraic means:
1)
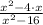 Given
Given
2)
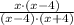 Associative, commutative and distributive properties/
Associative, commutative and distributive properties/
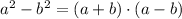
3)
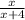 Commutative, associative and modulative properties/Existence of multiplicative inverse/Result
Commutative, associative and modulative properties/Existence of multiplicative inverse/Result
Now we evaluate the function for each value: