Question

A golfer hits a golf ball.

The function
d(t) = –2t2 + 7t + 4
most closely represents the height(h) of the golf ball in feet after t seconds. How
long is the golf ball in the air?

Answer 1

The golf ball was in the air for 4 seconds.

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

This polynomial has roots
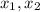`x_(1), x_(2)` such that
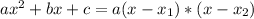`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\Delta))/(2*a)`

`x_(2) = (-b - √(\Delta))/(2*a)`

`\Delta = b^(2) - 4ac`

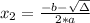
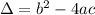
In this question:

We have to find the amount of time it takes for the ball to hit the ground. We have that:

`d(t) = -2t^2 + 7t + 4`

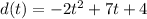
Which is a quadratic equation with
`a = -2, b = 7, c = 4`.

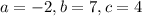How long is the golf ball in the air?

We have to find t for which
`d(t) = 0`

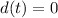
So

`-2t^2 + 7t + 4 = 0`

`\Delta = b^(2) - 4ac = (7)^2 - 4(-2)(4) = 81`

`t_(1) = (-7 + √(81))/(2*(-2)) = -0.5`

`t_(2) = (-7 - √(81))/(2*(-2)) = 4`

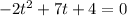
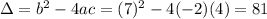
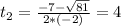
Time is a positive measure, so t = 4.

The golf ball was in the air for 4 seconds.