Question

A particle of unit mass moves so that displacement after t seconds is given by x = 2 cos (t - 2). Find the acceleration and kinetic energy at the end of 3 seconds. (K.E = (1/2) m v²)

Answer 1

a₃ = -1.08 m/s², K = 1.42 J

Step-by-step explanation:

The particle is in a periodic motion, so the general expression is

x = A cos (wt + Ф)

let's compare the terms with the expression they give us

x = 2 cos (t - 2)

the amplitude of motion is A = 2 m, the angular velocity w = 1 rad / s, and the phase is Ф = - 2.

to find the acceleration we use its definition

v = dx / dt

a = dv / dt

a =
`( d^2x)/(dt^2)`

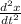
let's perform the derivative

v = - A w sin (wt + Ф)

a = - A w² cos wt + Ф)

substituting the values

a = - 2 1² cos (t-2)

for t = 3 s

a₃ = 2 cos (3-2)

remember angles are in radians

a₃ = -1.08 m/s²

To calculate kinetic energy, let's find the velocity for t = 3 s

v = - 2 sin (t-2)

v = -2 sin (3-2)

v = - 1.683 m / s

body mass is m = 1 kg

we calculate

K = ½ m v²

K = ½ 1 (-1.683) ²

K = 1.42 J