Question

A museum conducts a survey of its visitors in order to assess the popularity of a device which

is used to provide information on the museum exhibits. The device will be withdrawn if fewer
than 20% of all of the museum’s visitors make use of it. Of a random sample of 100 visitors,
15 chose to use the device.
i. Carry out an appropriate hypothesis test at the 5% significance level to
see if the device should be withdrawn and state your conclusions.
ii. Calculate the p-value of the test

Answer 1

i:

The appropriate null hypothesis is
`H_0: p \geq 0.2`

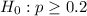
The appropriate alternative hypothesis is
`H_1: p < 0.2`

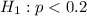
The p-value of the test is 0.1057 > 0.05, which means that there is not sufficient evidence that fewer than 20% of the museum visitors make use of the device, and so, it should not be withdrawn.

ii:

The p-value of the test is 0.1057

Explanation:

Question i:

The device will be withdrawn if fewer than 20% of all of the museum’s visitors make use of it.

At the null hypothesis, we test if the proportion is of at least 20%, that is:

`H_0: p \geq 0.2`

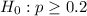
At the alternative hypothesis, we test if the proportion is less than 20%, that is:

`H_1: p < 0.2`

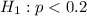
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.2 is tested at the null hypothesis:

This means that
`\mu = 0.2, \sigma = √(0.2*0.8) = √(0.16) = 0.4`.

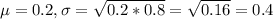The device will be withdrawn if fewer than 20% of all of the museum’s visitors make use of it. Of a random sample of 100 visitors, 15 chose to use the device.

This means that
`n = 100, X = (15)/(100) = 0.15`

Test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.15 - 0.20)/((0.4)/(√(100)))`

`z = -1.25`

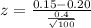
P-value of the test and decision:

The p-value of the test is the probability of finding a sample proportion below 0.15, which is the p-value of z = -1.25.

Looking at the z-table, z = -1.25 has a p-value of 0.1057.

The p-value of the test is 0.1057 > 0.05, which means that there is not sufficient evidence that fewer than 20% of the museum visitors make use of the device, and so, it should not be withdrawn.

Question ii:

The p-value of the test is 0.1057