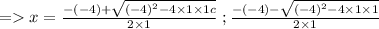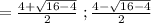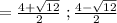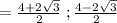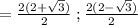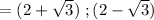Question

What are the roots of the polynomial x2 - 4x + 1 ?

Work out your answer on our whiteboard. Then, click the buttons below to
see the step-by-step solution.

Answer 1

x = (2 + √3) , (2 - √3)

Explanation:

GIVEN :-

• A quadratic polynomial x² - 4x + 1

TO FIND :-

• Roots of the quadratic polynomial

GENERAL FORMULAE TO BE USED IN THIS QUESTION :-

Quadratic formulae -

For a polynomial ax² + bx + c , its roots are :-

`x = (-b + √(b^2 - 4ac) )/(2a) \; ; (-b - √(b^2 - 4ac) )/(2a)`

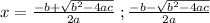
SOLUTION :-

Use the quadratic formulae to find the roots of the polynomial.

`=> x = (-(-4) + √((-4)^2 - 4 * 1 * 1c) )/(2 * 1) \; ; (-(-4) - √((-4)^2 - 4 * 1 * 1) )/(2 * 1)`

`= (4 + √(16 - 4) )/(2) \; ; (4- √(16 - 4))/(2)`

`= (4 + √(12) )/(2) \; ; (4- √(12))/(2)`

`= (4 + 2√(3) )/(2) \; ; (4- 2√(3))/(2)`

`= (2(2 + √(3)))/(2) \; ; (2(2- √(3)))/(2)`

`= (2 + √(3) ) \; ; (2 - √(3) )`