Find the first derivative of the following: f(x)=e^{x³}

Question

asked Apr 2, 2022 44.8k views

2 Answers

VoidPointer · Answer 1 · 2022-04-03T14:08:45+0000

Answer:

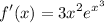
$\displaystyle f'(x) = 3x^2 {e}^{ {x}^(3) }$

Explanation:

we would like to figure out the first derivative of the following:

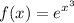
$\displaystyle f(x) = {e}^{x ^(3) }$

to do so take derivative In both sides:

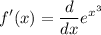
$\displaystyle f'(x) = (d)/(dx) {e}^{x ^(3) }$

to differentiate the above we can consider composite function derivation given by

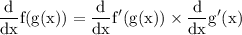
$\rm\displaystyle (d)/(dx) f(g(x)) = (d)/(dx) f'(g(x)) * (d)/(dx) g'(x)$

let

g(x)=u

so we obtain:

$\displaystyle f'(x) = (d)/(dx) {e}^(u) * (d)/(dx) u$

substitute back:

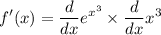
$\displaystyle f'(x) = (d)/(dx) {e}^{ {x}^(3) } * (d)/(dx) {x}^(3)$

by using derivation rule we acquire:

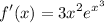
$\displaystyle f'(x) = 3x^2 {e}^{ {x}^(3) }$

and we are done!