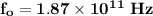Answer:
Step-by-step explanation:
Answer:
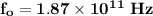
Step-by-step explanation:
The formula for calculating the elastic potential energy is:
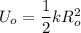
By rearrangement and using (K) as the subject;
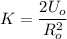
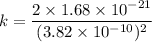
k = 2.3 × 10⁻² N/m
Now; the formula used to calculate the frequency of the small oscillation is:
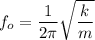
where;
m = mass of each atom
assuming
m = 1.66 × 10⁻²⁶ kg
Then: