Question

Please use the following image for the next 7 questions. Keep in mind

that because XY is tangent to circle M, XY and XM form a right angle. XY is tangent to circle M at point X.

XM = 12 and YM = 43.


Questions:

1. What is the area of circle M?

2. What is the circumference of circle M?

3. Find the length of XY.

4. Find the measure of angle M.

5. Find the area of triangle XYM.

6. Find the area of the minor sector that has been created as a part of triangle XYM.

7. Find the arc length of the minor arc from point C to the point where YM intersects with the circle.

Answer 1

Explanation:

1). Since, XM is the radius of the circle,

Therefore, area of the circle =
`\pi r^(2)`

=
`\pi (XM)^2`

=
`\pi (12)^2`

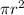
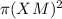
= 452.39 units²

2). Circumference of a circle = 2πr

= 2π(XM)

= 2π(12)

= 24π

= 75.40 units

3). By applying Pythagoras theorem in ΔYXM,

YM² = XY² + XM²

(43)²= (XY)² + (12)²

1849 - 144 = (XY)²

XY = 41.29 units

4). tan(∠M) =
`\frac{\text{Opposite side}}{\text{Adjacent side}}`

=
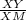
`(XY)/(XM)`

m∠M =
`tan^(-1)((41.29)/(12) )`

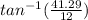
= 73.79°

5). Area of ΔXYM =
`(1)/(2)(\text{Base)}(\text{Height})`

=
`(1)/(2)(41.29)(12)`

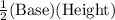
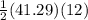
= 247.74 square units

6). Area of the minor sector created by ΔXYM =
`(\theta)/(360)(\pi r^2)`

=
`(73.79)/(360)(452.39)`

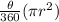
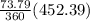
= 92.73 units²