Question

Can someone help with this problem! Please don't scam

Answer 1

KQ = 11.5 units

Explanation:

In triangle ABC,

K is the point of intersection of medians AP and BQ.

Therefore, point K will be the centroid of the triangle.

Property of the centroid of a triangle,

" Centroid of a triangle divides the median in the ratio of 2 : 1"

Ratio of BK and KQ = 2 : 1

`(BK)/(KQ)=(2)/(1)`

`(23)/(KQ)= (2)/(1)`

`KQ = (23)/(2)`

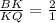
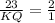
KQ = 11.5

Therefore, length of segment KQ = 11.5 units