Question

Find the surface area of a square pyramid with side length 4 yd and slant height 6 yd.

Answer 1

The surface area of a square pyramid with side length, 4 yd and slant height, 6 yd is equal to 64 square yards.

In Mathematics and Euclidean Geometry, the surface area of a square pyramid with side length and slant height can be calculated by using this mathematical equation:

Surface area of square pyramid =
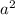`a^2` + 2al

• a represents the base edge of a square pyramid.
• h represents the height of a square pyramid.

By substituting the given side length and slant height into the formula for the surface area of a square pyramid, we have the following:

Surface area of square pyramid =
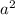`a^2` + 2al

Surface area of square pyramid =
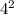`4^2` + 2 × 4 × 6

Surface area of square pyramid = 16 + 48

Surface area of square pyramid = 64 square yards.

Answer 2

112 yd²

Explanation:

Surface area of the square pyramid = area of base + perimeter of base × slant height

Area of base = s²

s = 4 yd

Area = 4² = 16 yd²

Perimeter = 4(s)

Perimeter = 4(4) = 16 yd

Slant height = 6 yd

Surface area of the square pyramid = 16 + 16 × 6

= 16 + 96

= 112 yd²